...by Tom Waineo
The Foucault knife edge test is a null test for a spherical mirror
at radius. Any error visible is a defect in the wavefront being
tested. A null means zero or nothing to measure. It is possible to
produce a quality spherical mirror which can be used in turn to null
a paraboloid. As before a visible error is a defect in the paraboloid
surface and thus the wavefront undergoing the knife edge test. Since
both mirrors are used at foci whereby they have spherical aberration,
a null is produced when those sphericals cancel. The author has used
the test for more than 25 years and presented in a article in
Telescope Making #11 and followed by Ed Jones in the July 1992 issue
of Sky & Telescope. What is now being presented is a update of my
experience in using the test.
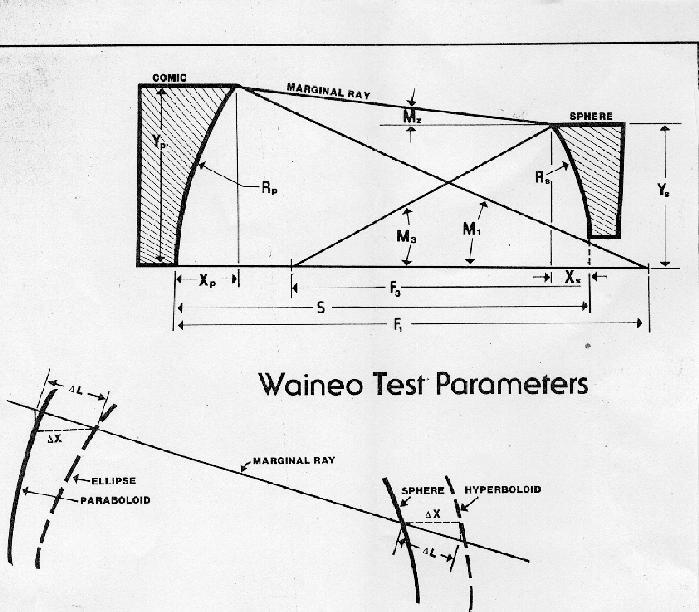
The size of the sphere has a
affect on the sensitivity of the null. A small sphere requires a
shorter radius and a greater focal reduction to achieve a null than a
larger sphere. The best results is with a sphere of at least 1/2 the
paraboloid in size and a radius of 10 to 12 diameters. The test is
unique since the light source and knife edge are seperated, but on
the test axis. The source to sphere distance is always less then half
the sphere radius. The distance from the paraboloid to knife edge
falls between the radius and focal length. The seperation of the
mirrors is less than this distance so that the knife edge is behind
the hole in the sphere to make the test possible. When a F/5 sphere
is tested at radius, the test cone has a diameter/radius ratio of 10.
A null test of a F/5 paraboloid can be made at focus using a flat to
return the projected light back to the paraboloid for a return to
focus. The sensitivity of the knife edge test varies inveresly with
the square of the focal or radius ratio. A F/5 has 1/4 that of a
R/10, but because of the double pass, it is twice the 1/4 or now 1/2.
The same sensitivity can be obtained by testing at F/7.07 which when
squared is 1/2 of the R/10 squared. Such a null can be made by using
a sphere of at least 1/2 of the paraboloid diameter. Needless to say
that it is easier to make the sphere than a full sized flat for the
same test sensitivity.
The test for a 16 inch F/5 uses a 9
inch diameter centered on the 12 1/2 inch sphere of 116 5/8 inch
radius. Ed Jones program was used to design the null test and
confirmed by a ray tracing program. The light source, spherical
mirror and knife are are mounted together on a adjustable stand. The
light source distance to the spheriucal mirror and the knife edge set
at the distance behind the mirror. A tape measure is accurate enough
to set those distances. Since a sphere has no optical axis, it must
be set square to the line of source and the center of the sphere. By
placing a eye behind the light source, adjust the source so that the
center of the sphere, the light reflection by the sphere and the
source falls in a line regardless of how the eye is placed. This is
also done with the source turned 180 degrees to face the mirror.
Adjustment is done by viewing behind the hole and aim at the mirror
center with the test stand unit. Then the mirror stand is adjusted so
the center, source, and source reflection all are on a straight line.
Now return the source to face the sphere and if all is done
accurately, a return from the paraboloid now passes thru the hole. It
may look complicated, but once done, the procedure is easily followed
and further set ups is done in a few minutes.
If all is set as
per null design parameters, then the knife edge is at the focus point
of the null. If it is not, move the whole source, sphere, and knife
stand unit until the cut off is at the focal point. The seperation of
the two mirrors is the least critical of the design parameters. If a
shadow starts from the center and moves to the edge or begins at both
edges and advances to the center, than there is coma present. If so
double check the alignment. Note the blockage of light caused by the
source support. the first is the light passing between the mirrors
and the second is after reflection by the paraboloid on route to the
knife edge. The two shadows need to be combined into one. The cut off
should be uniform. If errors are seen, the slopes are evaluated as if
testing a sphere at radius.
The null can help to test a large
low focal ratio mirror when the Foucault sampling of points across a
diameter has two sources of error. One is the tester's ability to
make precise measurements. The second is the number of zones measured
could not accurately give a wavefront error profile. The null gives a
infinite number of points to assure profile smoothness. Even when a
perfect null is obtained, it only means that the slope errors are so
small that the eye could not detect variations of shadows and lights.
Since there is nothing measurable, it assures smoothness of whatever
wavefront error is undetected. There is no need to null a 6 inch F/8
for the Foucault test at radius is accurate. For a 10 inch F/5 or
larger mirrors, it is nice knowing that a null is available if you
ever need it for quality assurance.
The enclosed images show a
16" f/5 being tested by a 12.5" sphere (9" of which is
in use).
more notes by Tom W:
I have been using this
null for 25 years. In the shops, there are many spheres used for the
Hindle test of Cassegrain secondaries and for Ritchey Common testing
of flats. With those mirrors avilable, they could be used to test
conics. I have 4 spheres of my own. A 5 of 51 radius, a 8 of 127
rad,a 12.5 of 116 rad, and a 11.5 of 29.5 rad that can be used for
testing. I have two projects now. One is to convert the optics of a
Celestron Comet Catacher Schmidt Newtonian of 5.5 F/3.6 into a Wright
Newtonian. The other is a 17 inch F/7.5 Ritchey Chretien Cassegrain
with a F/2.8 primary. The Hindle sphere was used to test the
secondary and would be used to null the primary as well. I found that
the Cass will null a source at 100 ft with a increase of back focal
distance and mirror spacing. The 100 ft distance uses the full
aperture of the secondary whereas for the infinite focus, the
secondary is oversized and the edge could not be seen for testing.
The 100 ft distance test means I do not need to borrow a big flat and
I can use a PDI (Point Diffraction Interferometer). I bought a $40
bar code He Ne laser from H&R. This laser is the smallest I have
ever seen. It is only a inch diameter and 6 inch long for 1/2 mw. A
12 volt DC power supply that plugs in the wall powers it.