Notes on the simulation
Green means pointing accuracy is as good as the initialization accuracy. Red means that pointing errors exceed the maximum allowed pointing error. The two black dots represent the initialization stars.Latitude is set to 35 degrees North; Sidereal time is set at 00:00:00. The circle represents the sky with grid lines every 30 degrees.
The pointing errors are averaged for the number of Monte Carlo initializations, where each initialization is given random errors based on the maximum initialization error in degrees set by the user.
For example, if the maximum initialization error is set to one degree, then the initialization stars will have their altitude and azimuth altered by a random value between zero and one. The total angular error is the combined altitude and azimuth axis error. For instance, if the randomized altitude error happens to be 0.5 degrees and the randomized azimuth error happens to also be 0.5 degrees, then the angular error will be 0.7 degrees (the square root of 0.5^2 + 0.5^2).
Axis mis-alignment is the non-perpendicularity of the telescope's azimuth axis to its altitude axis. Imagine a Dobsonian styled telescope where one side of the rocker box is lower. The telescope will lean to one side as it is aimed upward. The altitude's pads may need to be shimmed on one side. In an equatorial telescope axis mis-alignment occurs when the Declination axis is not set at exactly 90 degrees to the Right Ascension axis. A shim may be needed in the saddle that holds the optical tube assembly.
Interestingly, for an altazimuth aligned telescope, axis mis-alignment can be substituted by azimuth offset, an offset that is often baked into alignment software. For example, an axis mis-alignment of 0.5 degrees can be compensated for by an azimuth offset of 0.2 degrees, reducing the pointing error by an order of magnitude (keeping in mind that we rarely aim at the horizon). For my simulator where you can investigate the relationship between axis mis-alignment and azimuth offset, see PriAxisMountErrors.htm
Comments
An altazimuth telescope needs to be aligned or initialized in order to track and find objects. Initialization between the telescope’s azimuth and altitude axes and the sky’s Right Ascension and Declination coordinates requires synchronizing on two different points in the sky. Each point is described by its equatorial coordinates (RA, Dec), the telescope’s coordinates at the moment the synchronization occurred (the telescope’s azimuth and altitude readings) and the sidereal time of the synchronization.Some believe that the initialization points should avoid the equatorial pole (e.g. the star Polaris for the northern hemisphere). But is this true? Some say that the initialization points should never be at the same telescope’s altitude. Some say that the init points should be 90 degrees apart. Some say that one init star should be in the general vicinity of where you will observe. Just how accurate do the initializations need to be? How are pointing errors distributed across the sky?
Think of the ideal and actual telescope to sky coordinate frames containing longitude and latitude lines like Earth. With real life errors, the ideal and actual frames are translated side to side (azimuth), translated up and down (altitude) and rotated or twisted with respect to each other. I used the matrix transformations with directional cosines as developed by Taki.
I chose seven initializations.
1. First point at the equatorial pole in the north and the second point on the meridian 90 degrees away facing south (Declination = 0).
2. First point at the telescope’s zenith or azimuth’s pole and the second point on the southern horizon.
3. First point on the northern horizon and second point on the southern horizon, both up one degree in altitude.
4. Two points that are as distantly separated as possible in all four coordinates: RA, Dec, azimuth and altitude.
5. Two points widely separated but at exactly the same telescope’s altitude.
6. Two points separated by 135 degrees.
7. Two points close in together, about 30 degrees apart, with some change in both azimuth and altitude.
I introduced errors into the initializations just like occurs at the eyepiece when aligning the telescope as the evening begins. I choose random errors varying from zero to one degree. These random errors are in both the telescope’s azimuth and altitude coordinates. Each initialization was evaluate for accuracy using 30 points across the sky, roughly separated by 30 degrees, from horizon to zenith, in all cardinal directions. I ran each initialization 100 times so as to build up a solid picture of the resulting telescope pointing errors.
| Style of initialization | Telescope pointing error in degrees |
| EquatPoleAndMeridian90DegAway | 0.7 |
| ZenithSouthHorizon | 0.6 |
| NorthSouthHorizon | 7.9 |
| FarthestApart | 0.7 |
| SameAlt | 0.7 |
| initAltaz135Apart | 0.8 |
| 30degApart | 1.2 |
Comments
1. The beginning random initialization errors were 0.7 degrees (0.5 degrees in each axis results in 0.7 degree angular error). The ending simulated telescope pointing errors for the best initialization strategies were the same. So, garbage in, garbage out.
2. Initializing using the equatorial pole is fine; not a bugaboo to be avoided.
3. Ditto for initializations at the same telescope altitude but separated in azimuth.
4. Using the horizon with initialization points essentially 180 degrees apart resulted in astonishing errors.
5. Telescope pointing error increases when the initialization points are close to each other.
Since telescope pointing errors increase with small and large initialization distances, is there a best distance?
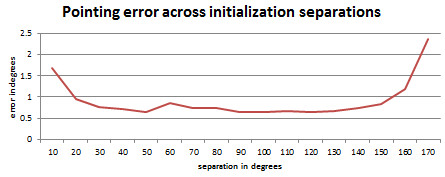
The idea that the initialization points should be 90 degrees apart is correct, however, initialization distances from 40 to 140 degrees separation performed nearly as well. As the separation approaches zero or 180 degrees, the error increases sharply. By the way, that small bump at the 55 degree separation point is an artifact of initializing near the telescope's azimuth pole aimed at the zenith.
Since portable altazimuth telescopes are initialized each evening, the errors will vary each night. How greatly the errors vary depends on initialization accuracy and on the angular separation of the initialization stars. Try the rapid fire random initialization to see how much more the pointing errors vary from night to night when the angular separation of the initialization stars is small. In fact the night to night variation is so great that it is the dominant feature.
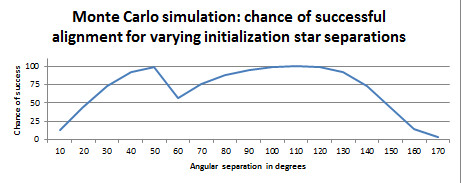
This study shows the chance of all sky pointing success across a range of initialization star separations. The dip at 55 degree separation is centered on the telescope's azimuth pole. This study suggests to stay away from the telescope's altazimuth pole and to keep a wide separation between the initialization stars.
And there are surprising patterns. Interestingly, the patterns seem to connect at the horizon, i.e., the error at any point on the horizon is mirrored across the sky to a point on the horizon 180 degrees away.
Lessons learned from the simuulator to apply in the field at night
--- It is most important is to make the initialization measurements with the two stars as accurately as possible. Use a high powered cross haired eyepiece.--- Best pointing accuracy usually occurs between two initialization stars and best chance of success comes when the stars are widely separated.
--- Axis mis-alignment, the non-perpendicularity of the telescope's azimuth axis to its altitude axis, affects pointing as the scope is aimed upward. Azimuth offset may compensate.
Background data
My data, code and details are incorporated in my QUnit unit tests available at https://bbastrodesigns.com/lib/coordLib%20unitTests.htm. See the test moodule named, "investigate different init points for accuracy given realworld errors".Mel Bartels, March 2014